The Power Of Compound Interest
What is Compound Interest?
Imagine a small snowball rolling down a snowy hill. With every turn, it picks up more snow, growing larger and faster as it descends. This is a simple yet powerful illustration of compound interest—a financial concept that can significantly boost your wealth over time. Just as the snowball grows by accumulating more snow, your investment grows by earning interest on both the original amount and the interest accumulated so far i.e. “interest on interest”
Let’s break it down with an example. Picture this: You invest ₹1,00,000 in a fixed deposit account offering 7% annual interest. In the first year, you earn ₹7,000 as interest on your original investment of ₹1,00,000. If you withdraw this ₹7,000, your account will still have only the ₹1,00,000 you started with. In the second year, you’ll earn another ₹7,000—this is called simple interest because your returns are based solely on the initial amount.
But what if you decide to reinvest the ₹7,000 interest back into your account instead of withdrawing it? Now your second-year interest isn’t calculated on ₹1,00,000 anymore—it’s based on ₹1,07,000 (the original amount plus the first year’s interest). This means your second-year interest grows to ₹7,490! By reinvesting, you’ve unlocked the compounding effect, where your money works harder for you by earning “interest on interest.”
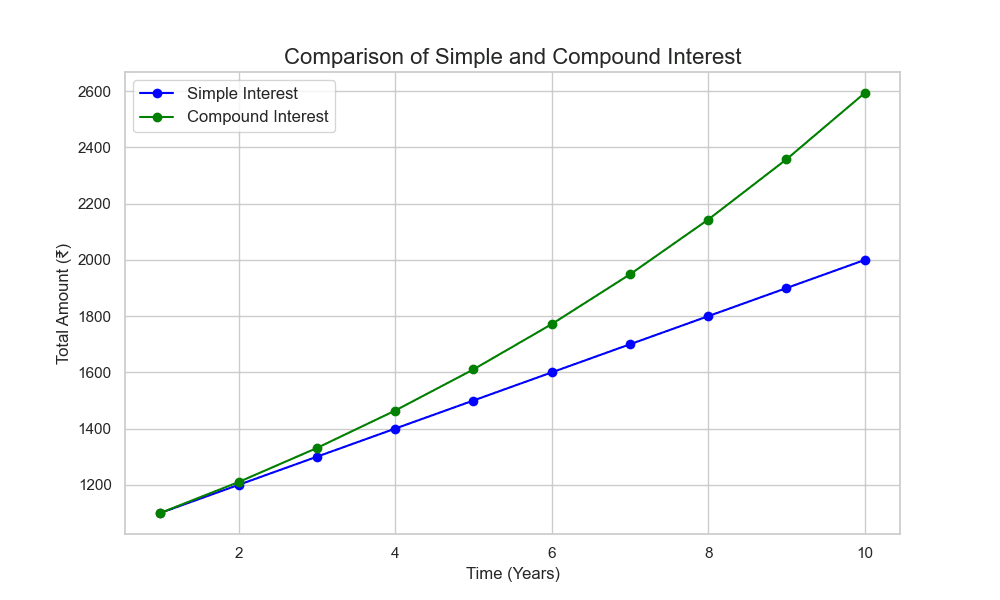
Simple Interest Vs Compound Interest
The chart below shows the difference in growth between simple interest & compound interest.
| Facts | Simple Interest | Compound Interest |
| 1. Interest Calculation | Interest is calculated only on the initial principal. | Interest is calculated on the initial principal as well as the accumulated interest. |
| 2. Growth Over Time | Linear growth: Interest remains constant throughout the investment period. | Exponential growth: Interest is reinvested and grows over time. |
| 3. Frequency of Compounding | No compounding: Interest is added to the principal once, periodically. | Interest is compounded periodically (e.g., annually, quarterly, monthly). |
| 4. Final Value | The final value is simply the sum of the principal and interest. | The final value is much higher due to interest on interest (compounding). |
How Time Turns Small Investments into Wealth
Over time, this power of compound interest becomes even more dramatic. With each passing year, your investment grows faster, just like the snowball gathering more snow. This is why compounding is often called the “eighth wonder of the world” in the financial world—it can turn modest investments into significant wealth if given enough time. As you can watch in the below GIF.
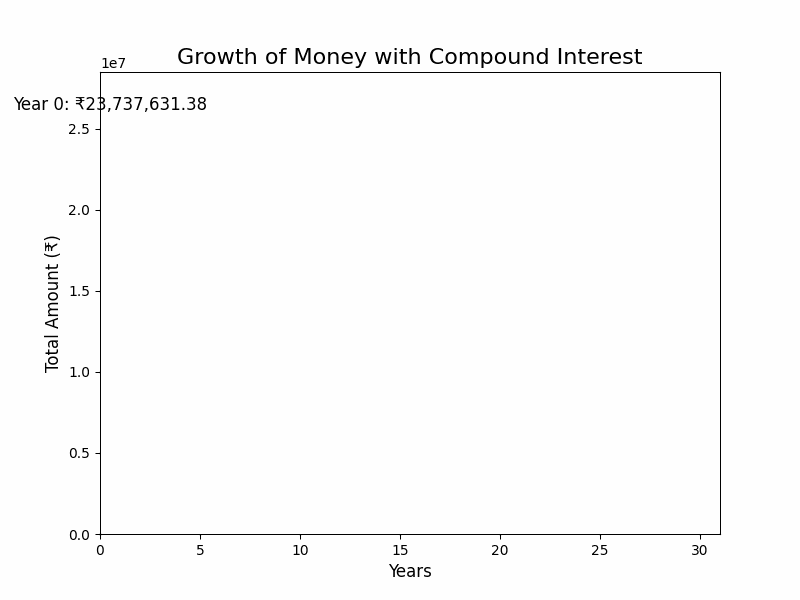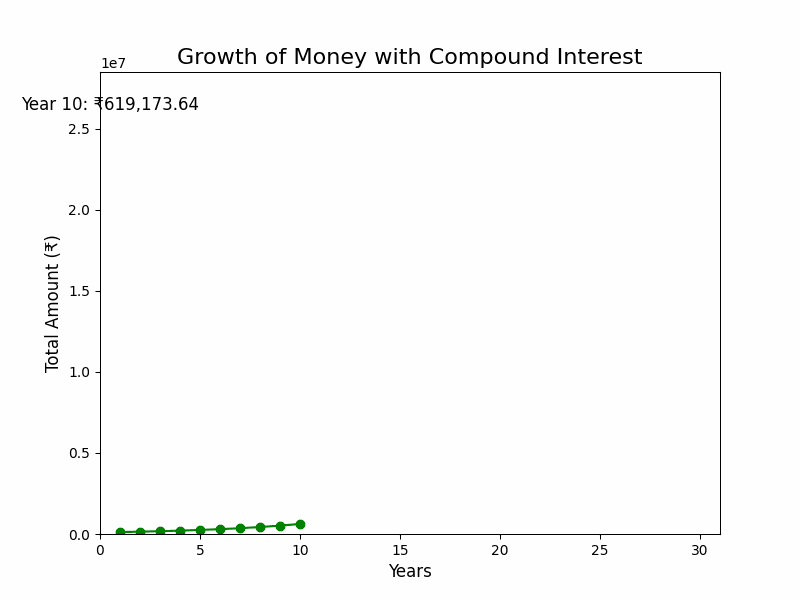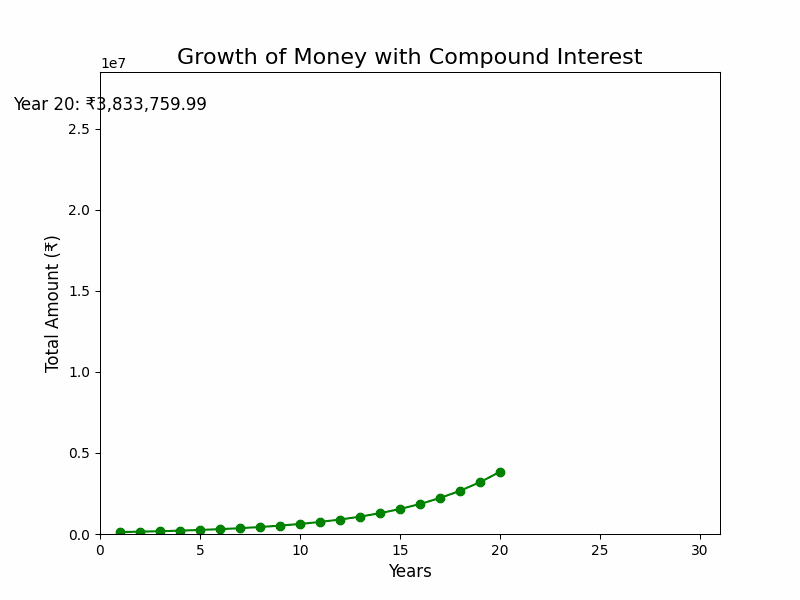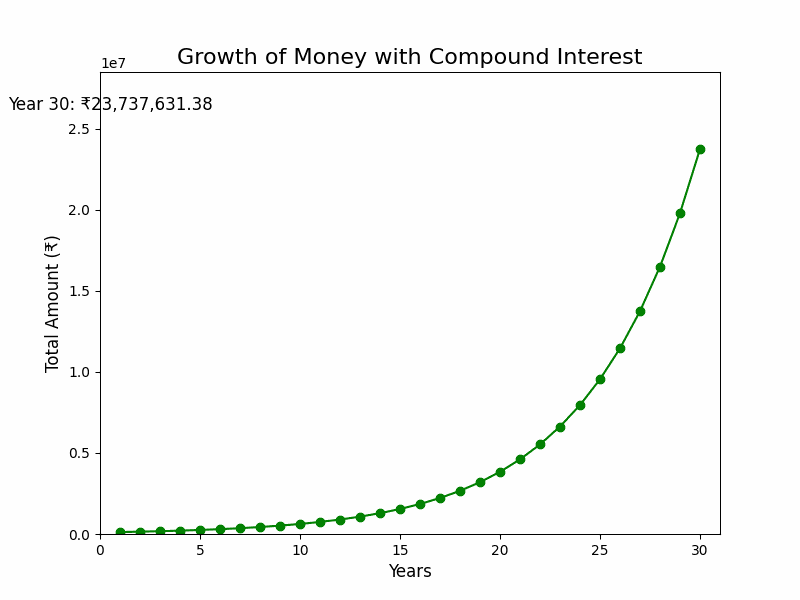
Imagine planting a small seed in a garden and watching it grow into a towering tree that bears fruit year after year. That’s the magic of compounding in investments. For instance, starting with just ₹1,00,000 and letting it grow at an assumed rate of 20% annually, your investment could snowball into an impressive ₹2.37 Cr over time. Sounds like magic, right? (like in the GIF shown above)
Compound Interest Calculator (or Cumulative Interest Calculator) -Lumpsum investment.
Compound Interest Calculator
But here’s the catch—it’s not magic, it’s time. The longer you let your investment grow, the more the power of compound interest. This is why starting early is so crucial. It gives your money more time to multiply and build wealth.
“Compound interest is the eighth wonder of the world. He who understands it, earns it … He who doesn’t … Pays it” – Albert Einstein
Think of it this way: every year your returns don’t just grow—they grow on top of the returns from previous years. It’s like building a staircase where each step gets taller than the last. Starting early could mean retiring earlier than most, with a financial cushion that lets you live on your terms. So, the best day to start investing was yesterday; the next best day is today. Give your money time, and let it work wonders for you!
FORMULAE FOR CALCULATING MATURITY AMOUNT USING COMPOUNDING EFFECT IN CASE OF LUMPSUM INVESTMENTS:
Formulae for calculating (power of compound interest) future value:
Compound Interest Formulae :
A = P (1 + r/n) ^nt
A = Maturity amount.
P = Initial amount of investment.
r = annual interest rate/ rate of return.
n = number of times the interest is compounded per year.
t = period the money is invested for.
Example uses the formula:
Inputs:
Investment: 1,00,000/-
Rate of Return: 7%
Time period: 5 Years
Output:
A = 1,00,000[(1+(0.07/1) ^1*5]
A = 1,00,000(1.402552)
A = 1,40,255
Hence total investment after 5 years compounded annually would be worth Rs. 1,40,255/-
Effect of Compounding in Regular SIP Investments for Long-Term Wealth
In India, the dream of a comfortable retirement is often a distant goal for middle-class individuals. But what if I told you that securing a financially independent future is not only achievable but surprisingly simple? For those with modest incomes, the key to unlocking this dream lies not in earning more but in starting early. This eighth wonder of the world requires patience and time to work its magic over time. This is how we utilize the real power of compound interest.
Imagine consistently investing ₹10,000 every month in a mutual fund for the long term. Over time, this monthly habit combined with compounding interest can lead to extraordinary growth. By the fifth year, your total contributions of ₹600,000 will grow to ₹805,873, giving you a 34% return on investment (ROI). As the years progress, the growth becomes even more significant. By the tenth year, your ₹1,200,000 investment will grow to ₹2,103,740, achieving a 75% ROI. At the 15th year, your total investment of ₹1,800,000 will more than double to ₹4,198,620, yielding a 133% ROI. By the 20th year, your investment will grow to ₹7,558,051, with an impressive 215% ROI, and by the 25th year, it will reach a remarkable ₹12,958,780, delivering a 333% ROI. This demonstrates how disciplined monthly investments of ₹10,000 can achieve massive wealth growth over time, even at a modest annual interest rate of 10%
Summarized Table:
| Year | Total Investment (₹) | Future Value (₹) | Return on Investment (ROI) |
|---|---|---|---|
| 5 | 6,00,000 | 8,05,873 | 34% |
| 10 | 12,00,000 | 21,03,740 | 75% |
| 15 | 18,00,000 | 41,93,968 | 133% |
| 20 | 24,00,000 | 75,60,300 | 215% |
| 25 | 30,00,000 | 1,29,81,812 | 333% |
Compound Interest Calculator (or Cumulative Interest Calculator) – Monthly Investments
SIP Calculator
It took approximately 13–15 years to double your money initially, but it only took the following 5 years for it to triple, and it will take even less years for your money to yield 3x and 4x returns. Over time, compounding acts like magic. “The longer the money is invested, the higher the returns”.
This is one of the reasons why every personal finance channel on YouTube will advise you to start investing early in your 20s, this gives you the freedom to do the job/work that you love and retire early.
I understand what you might be thinking—earning 1Cr over 25 years might not seem like much, but keep in mind that I only used a 10% rate in the example I provided. You can expect annual profits of 20% to 25% from wise investments. Let’s just assume that I invest Rs. 10,000 per month at a rate of 15% rather than 10% as in the previous example to see what my returns will be after 25 years:
| Year | Total Investment (₹) | Future Value (₹) | Return on Investment (ROI) |
|---|---|---|---|
| 5 | 6,00,000 | 9,30,449 | 55% |
| 10 | 12,00,000 | 28,01,913 | 133% |
| 15 | 18,00,000 | 65,66,097 | 265% |
| 20 | 24,00,000 | 1,41,37,214 | 489% |
| 25 | 30,00,000 | 2,93,65,436 | 879% |
By simply increasing the rate of return from 10% to 15%, your investment would increase by 8.79 times over the same length of time, as opposed to 3.33 times in the previous example. And this time, as you can see, by the end of 20 years your money will be 4.89 times (or 489%) of your initial investment instead of 25 years with just 5% increase in rate of return. We will also discuss the impact of this factor on our investments below.
🤔 Here’s a Quick Quiz for You!
If you invest ₹30,000 every month at 12% interest for 10 years, compounded half-yearly, how much will it grow? Drop your guesses in the comments, and I’ll share the answer! 🙌
The Magic of Compounding: Key Factors for Exponential Growth
1. Time: How long do you keep your money invested?
The longer the money gets invested the higher the returns will be. Go for long term investing for creating wealth, you will get the best return on investment.
Example:
| Period | Investment | Rate | Maturity Amount |
|---|---|---|---|
| 5 | 6,00,000 | 15% | 9,30,449 |
| 10 | 12,00,000 | 15% | 28,01,913 |
| 15 | 18,00,000 | 15% | 65,66,097 |
| 20 | 24,00,000 | 15% | 1,41,37,214 |
| 25 | 30,00,000 | 15% | 2,93,65,436 |
The above table Demonstrates how the maturity amount changes over time while keeping the investment amount and rate of return constant year on year.
2. Compounding rate: How much is your yearly Return on Investment (ROI)?
Your returns vary a lot with the change in ROI, as we discussed in the above paragraph, a slight change in rate of return will have a great impact on your investments.
| Period | Investment | Rate | Maturity Amount |
|---|---|---|---|
| 10 Years | 12,00,000 | 7% | 17,74,032 |
| 10 Years | 12,00,000 | 10% | 21,03,740 |
| 10 Years | 12,00,000 | 15% | 28,01,913 |
| 10 Years | 12,00,000 | 20% | 37,38,050 |
| 10 Years | 12,00,000 | 25% | 49,87,935 |
3. Tax rate: Brokerage charges & STCG & LTCG.
As per the Indian Income Tax Act 1961, the revised special tax rates applicable on long-term capital gain (LTCG) arising on the sale of investments shall be 12.5% (as proposed in budget 2024). This could have an impact on your maturity amount.
The maturity amount of your investments after 10 years will be Rs.28,01,913, and your initial investment is Rs.12,00,000. 20% of the profit from your investment, which is Rs.2,00,239.125 (12.5% of Rs.16,01,913 – the difference between Rs.28,01,913 and Rs.12,00,000), will be deposited with the government as tax.
Reduce the high number of transactions or frequent buying and selling of stocks or mutual funds in a single day or month. This will increase your brokerage charges.
Going for long-term investments will give you a major relief over short-term investments. This can be one of the best options if you don’t want taxes to eat your returns & the magic of compound interest.
How frequently money should be compounded for greater growth:
Compounding can also happen quarterly, monthly, weekly & daily. For instance, credit card debt compounds daily if payment is delayed, and becomes a huge liability in a very short time. The less frequently your money compounds the higher the power of compound interest.
The more often your money compounds the more high returns in the long term. This can make a huge difference in your maturity amount. The below table helps you to understand the impact.
| Years | Frequency | Rate | Investment | Maturity |
|---|---|---|---|---|
| 5 | Monthly | 3% | 12,00,000 | 70,69,924 |
| 5 | Quarterly | 3% | 12,00,000 | 21,67,333 |
| 5 | Yearly | 3% | 12,00,000 | 13,91,129 |
Compound interest can work against you?
Yes, compound interest works against you in cases of debt. Regardless of the source of your loan—a bank, financial institution, or other third party—you will be responsible for paying finance costs, or interest. You will be required to pay interest on both your principal and the interest you have skipped if you neglect to make your interest payment.
The primary issue is credit cards; if interest is not paid on time, it will compound daily, resulting in exorbitant interest rates that could jeopardize your credit score. Here the power of compound interest is working against you.
Real-life applications of compound interest:
- Savings Accounts: When you deposit money in a savings account, banks often pay interest on your balance. With compound interest, you earn interest on the interest already accumulated, leading to exponential growth of your savings over time.
- Investments: In investments like stocks, bonds, or mutual funds, compound interest helps your returns grow faster. Reinvested dividends and interest contribute to the overall growth of your investment portfolio.
- Loans and Mortgages: When you take out a loan or mortgage, the amount you repay includes compound interest. This means you pay interest on both the principal and the interest that has accrued, which can make loans more expensive over time.
- Bonds: Bonds often pay interest periodically. Reinvesting the interest earned can lead to compound growth of your investment in the bond.
- Insurance Products: Some insurance products, like whole life insurance or certain annuities, use compound interest to grow the cash value of the policy over time.
- Business Growth: Businesses use the power of compound interest for various financial strategies, including reinvesting profits. This reinvestment can lead to accelerated growth and increased value of the business.
Conclusion
Compounding effect if given enough time, can break your financial barriers in one go. Best investors like Warren Buffet, known as a value investor, gained enormous wealth with the help of compounding and became one of the world’s wealthiest people. Even with a small amount you have to start investing early to gain the advantage of compounding. If you choose to invest a little later than your 20s, you have to save and invest a big amount to achieve the same level of growth with compounding.
What’s more important to you—starting early with small amounts or investing big but later in life?